5. seminář - Propojené datové struktury 2

Stromy

Analogickým způsobem, jako jsme vytvořili obousměrný spojový seznam, je možné vytvořit i komplexnější datové struktury. Na tomto semináři si stručně představíme, jak je možné naprogramovat pomocí uspořádané trojice binární strom. Binární strom je abstraktní datová struktura uchovávající data v uzlech, které obsahují samotná data a odkazy na další prvky binárního stromu: levý potomek a pravý potomek.

Uzel stromu budeme opět reprezentovat seznamem (uspořádanou trojicí), ve které první prvek uchovává hodnotu uzlu, druhý a třetí prvek obsahují reference na potomky.

    node = [42, [], []]

Binarni strom

Speciálním případem je uspořádaný binární strom, ve kterém jsou prvky stromu lineárně uspořádány dle hodnoty uzlu. Levý potomek obsahuje hodnotu menší než hodnota uložená v daném uzlu a pravý potomek obsahuje hodnotu větší než je hodnota uložená v daném uzlu. Například.

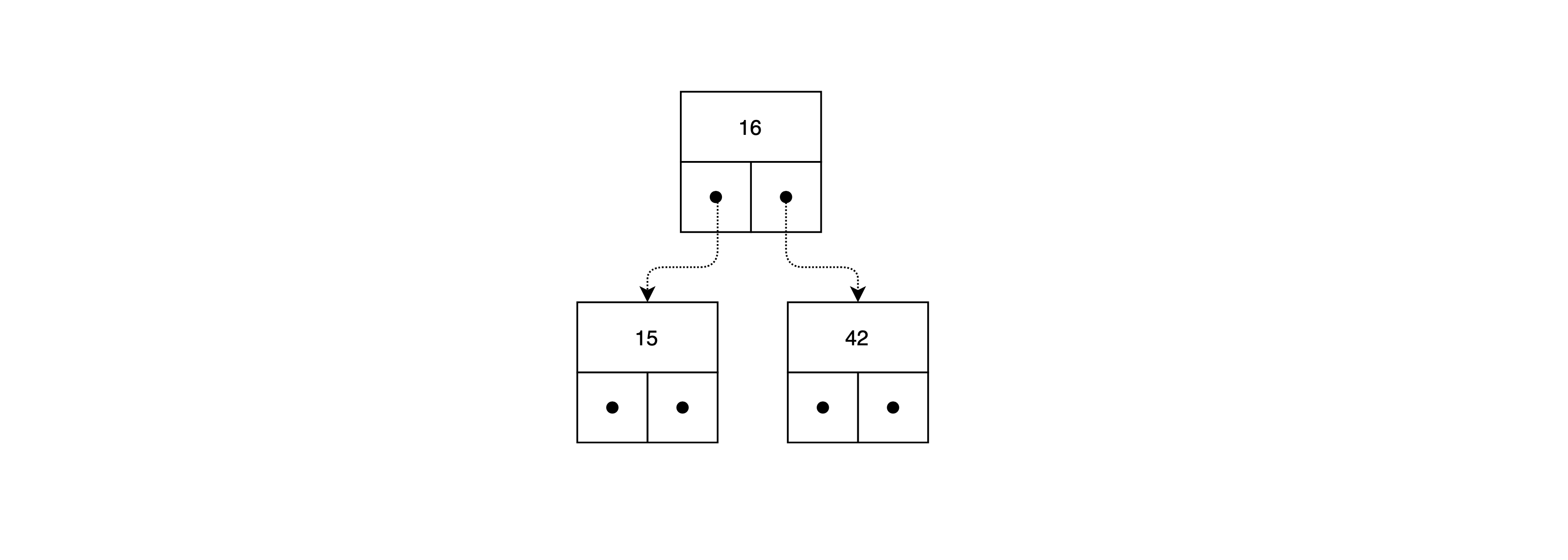
Tento strom odpovídá následujícímu seznamu.

    root = [16, [15, [], []], [42, [], []]]

Funkce vytvářející uspořádaný binární strom by mohla vypadat takto.

    VALUE = 0
    LEFT_CHILD = 1
    RIGHT_CHILD = 2
    
    def tree_add(node, x):
        if not node:
            node.extend([x, [], []])
            return
            
        while node[VALUE] != x:
            if x < node[VALUE]:
                if node[LEFT_CHILD]:
                    node = node[LEFT_CHILD]
                else:
                    node[LEFT_CHILD] = [x, [], []]
                    return
                    
            elif x > node[VALUE]:
                if node[RIGHT_CHILD]:
                    node = node[RIGHT_CHILD]
                else:
                    node[RIGHT_CHILD] = [x, [], []]
                    return
                    
    # Priklad pouziti
    
    root = []
    # přidání prvků do stromu
    tree_add(root, 8)
    tree_add(root, 4)
    tree_add(root, 16)
    tree_add(root, 15)
    tree_add(root, 42)
    tree_add(root, 23)

Grafy

Pomocí provázaných datových struktur je rovněž možné v jazyce Python snadno implementovat grafy, byť tento způsob reprezentace nemusí být vždy ten nejvhodnější. Následující příklad ukazuje reprezentaci neorientovaného grafu pomocí propojené datové struktury, přičemž každý uzel grafu je reprezentován jménem a seznamem sousedů.

    LABEL = 0
    EDGES = 1
    
    # přidání uzlu
    def add_node(graph, label):
        graph.append([label, []])
        
    # přidání neorientované hrany
    def add_edge(graph, from, to):
        for node in graph:
            if node[LABEL] == from:
                v = node
            elif node[LABEL] == to:
                w = node
            
        v[EDGES].append(w)
        w[EDGES].append(v)

    # Pouziti
    
    graph = []
    # přidání uzlů do grafu
    add_node(graph, "a")
    add_node(graph, "b")
    add_node(graph, "c")
    
    # přidání hran do grafu
    add_edge(graph, "a", "b")
    add_edge(graph, "a", "c")
    add_edge(graph, "c", "b")

Úkoly