2. seminář - Rekurze

Rekurze

Rekurzivní funkce

Pojem rekurze, v programování, označuje situaci, kdy funkce volá ve svém těle sebe sama. Rekurze obvykle umožňuje jednoduché řešení problémů, které je možné rozložit na menší podproblémy. Klasickým příkladem používající rekurzi je výpočet n-tého členu Fibonacciho posloupnosti.

    # výpočet n-tého členu Fibonacciho posloupnosti
    # rekurzivní výpočet
    def fib(n):
      if n <= 1: # limitní podmínka
        return n
      return fib(n - 1) + fib(n - 2) # rekurzivní volání

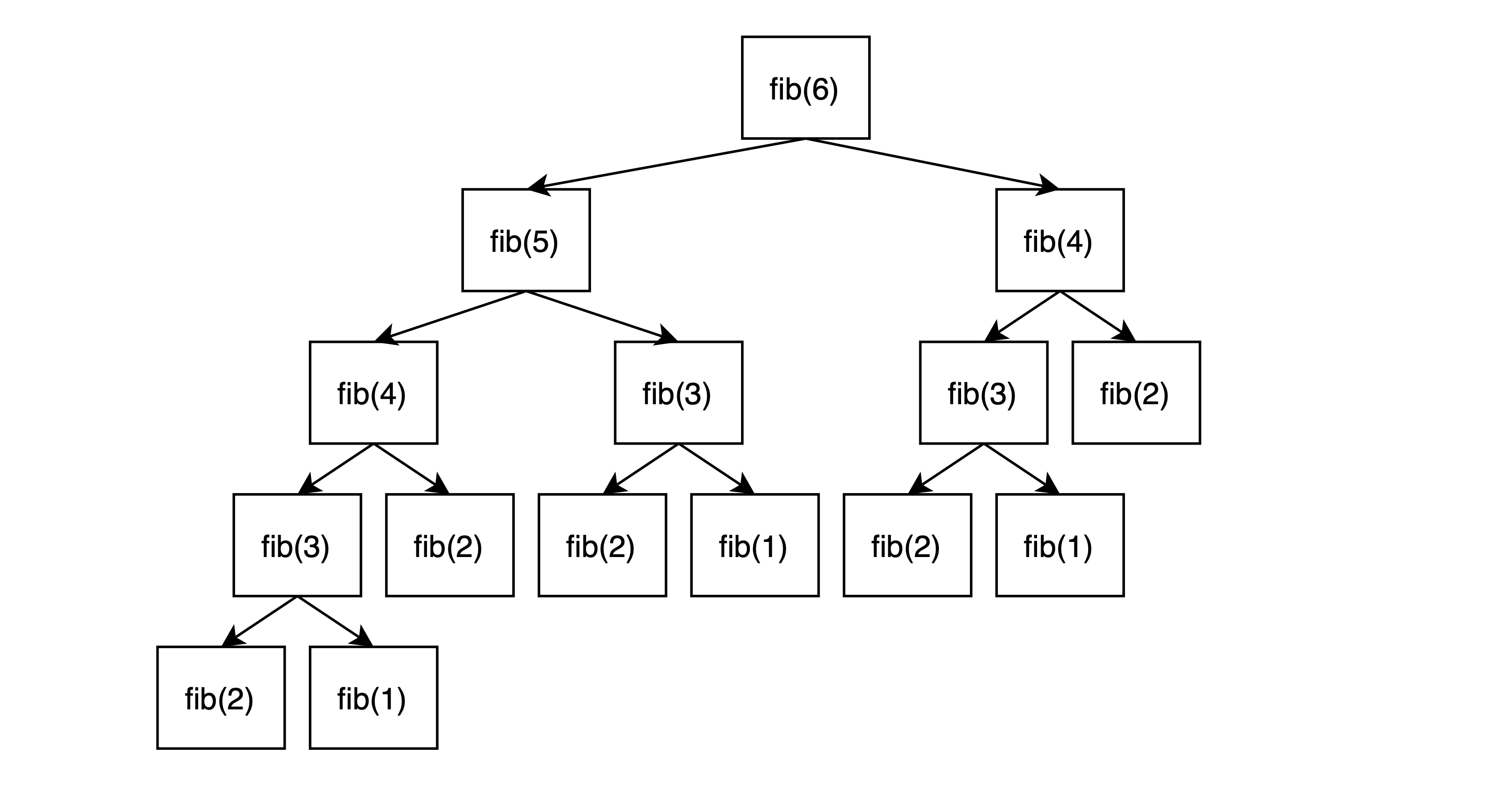
Pokud funkce obsahující rekurzi, jsou označovány jako rekurzivní funkce. Každá rekurzivní funkce obsahuje limitní podmínku, která určuje zda má dojít k opětovnému (rekurzivnímu) volání či nikoliv. Obrázek níže zachycuje průběh rekurzivního volání pro fib(6). Tento průběh se také označuje jako strom rekurzivního volání.

Iterativní funkce

Rekurzivní funkce jsou obvykle jednodušší a kratší než jejich iterativní protějšky. Následující zdrojový kód zachycuje iterativní verzi funkce fib.

    # výpočet n-tého členu Fibonacciho posloupnosti
    # iterativní verze
    def fib(n):
      prvni_clen = 0
      druhy_clen = 1
      for i in range(0, n):
        pomocna = prvni_clen
        prvni_clen = druhy_clen
        druhy_clen = pomocna + druhy_clen
      return prvni_clen

Rekurzivní verze je přímočařejí. Nevýhodou je paměťová náročnost rekurze. V případě výpočtu fibbonaciho posloupnoti narůstá počet rekurzivních volání exponenciálně zhledem k n. Řešením je použít koncovou rekurzi, kde není nutné čekat na výpočet jiného rekurzivního volání.

    # výpočet n-tého členu Fibonacciho posloupnosti
    # koncová rekurze
    def fib(n, prvni_clen, druhy_clen):
      if n < 1:
        return prvni_clen
      return fib(n - 1, druhy_clen, prvni_clen + druhy_clen)
      
    print(fib(6, 0, 1))

Úkoly

    # Pacaluv trojuhelnik
    
                 1
               1   1
             1   2   1
           1   3   3   1
          1  4   6   4   1
        1   5  10  10   5  1
      1   6  15  20  15  6   1
      
   # Přiklady volání
   pascal(0, 0) # -> 1
   pascal(3, 3) # -> 1
   pascal(6, 2) # -> 15