4. seminář - Rekurzivní funkce

TEACHING ❯ ZPC2

Rekurze

Rekurzivní funkci v jazyce C definujeme stejně jako nerekurzivní. Rozdílem je, že rekurzivní funkce obsahuje v těle volání sama sebe. Jsou svým použítím podobné cyklům. Musí stejně jako cykly obsahovat limitní podmínku. Rekurze je ve většině případuů pomalejší, ale může být přehlednější. Příkladem rekurzivní funkce může být výpočet faktoriálu který je definován předpisem:

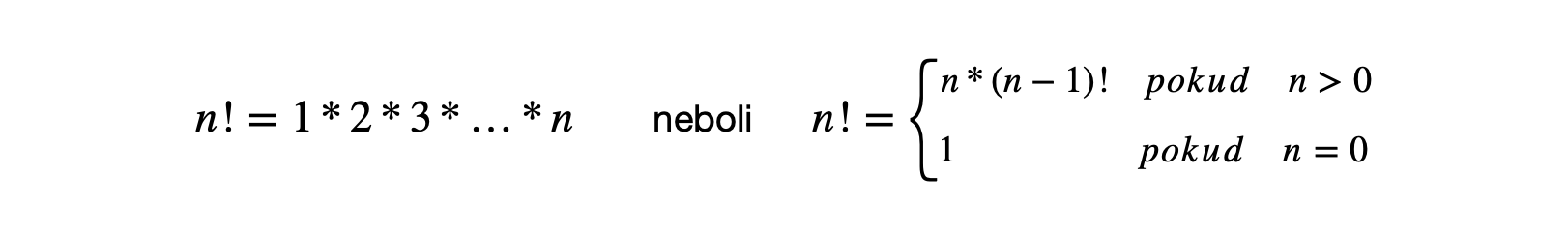
factorial equation

Implementace v C


    int factorial(int n) {
        // Limintni podminka
        if (n == 0) { 
            return 1; 
        }
        // Rekurzivni volani
        return n * factorial(n - 1);
    }

Průběh výpočtu


    // Výpočet faktrorial(5);
    factorial(5)
    5 * (factorial(4))
    5 * (4 * (factorial(3))))
    5 * (4 * (3 * (factorial(2))))
    5 * (4 * (3 * (2 * (factorial(1)))))
    5 * (4 * (3* (2 * (1 * (factorial(0))))))
    5 * (4 * (3* (2 * (1 * (1)))))
    5 * (4 * (3* (2 * (1))))
    5 * (4 * (3* (2)))
    5 * (4 * (6))
    5 * (24)
    120

Nalezení hodnoty v poli - cyklus


    int index_of_value(int value, int numbers[], size_t size) {
        for (int i = 0; i < size; i += 1) { 
            if (numbers[i] == value) {
                return i;
            }
        }
        return -1;
    }
    
    int main() {
        int numbers[] = {2, 3, 0, 5, 4};
        printf("%i\n", index_of_value(0, numbers, 5)); // 2
    }

Nalezení hodnoty v poli - rekurze


    int index_of_value(int value, int array[], size_t size) {
        return index_of_value_recursion(value, array, size, 0);
    }
    int index_of_value_recursion(int value, int array[], size_t size, int i) {
        if (i >= size) { // Je jiz index i vetsi nez je delka pole?
            return -1; // V tom pripade jsme prvek nenasli
        else if (array[i] == value) {
            return i;
        }
        index_of_value_recursion(value, array, size, i + 1);
    }
    
    int main() {
        int numbers[] = {2, 3, 0, 5, 4};
        printf("%i\n", index_of_value(0, numbers, 5)); // 2
    }

Stromová rekurze


    int fibbonaci(int n) {
        if (n <= 1) {
            return n;
        }
        return fibbonaci(n - 1) + fibbonaci(n - 2)
    }

Úkoly

Naprogramujte rekurzivní funkci mocnina(zaklad, exponent) vracející hodnotu zakladexponent.
Napište „hloupou“ rekurzivní funkci na výpočet součtu prvků intervalu celých čísel, kde interval je reprezentován pomocí 2 hodnot begin a end.
Napište rekurzivní funkci pro výpočet délky seznamu z minulého semináře.
Napiště rekurzivní funkci pascal která vypočítá daný prvek pascalova trojúhelníka.

Výpočet

Každý řádek (kromě prvního) má o jeden prvek víc než předchozí řádek. Řádky vždy začínají a končí jedničkou, ostatní čísla se vypočítají jako součet dvou čísel ležících nad nimi. (Z obrázku by to mělo být vidět; trojúhelník samozřejmě pokračuje směrem dolů donekonečna). Řádky i prvky v nich budeme číslovat od nuly, takže například prvek na řádku číslo 6 (tedy na sedmém řádku), který má na tom řádku pozici 2 (je tedy na řádku třetí), je 15. 


    # Pacaluv trojuhelnik
    
                 1
               1   1
             1   2   1
           1   3   3   1
          1  4   6   4   1
        1   5  10  10   5  1
      1   6  15  20  15  6   1
      
   # Přiklady volání
   pascal(0, 0) # -> 1
   pascal(3, 3) # -> 1
   pascal(6, 2) # -> 15